Table of Contents
Armadillo Calibration
Odometri constants
It is assumed that the turningpoint for the belts is the center of the belts.
cl = 0.00348377 cr = 0.003193242 w = 1.68336
UMB-mark test
UMB test (168 KB) Data and calculation showed in this page
Where am I? Sensors and Methods for Mobile Robot Positioning:
Download book from University of Michigan (12.2 MB)
Chapter 5 is used as the base for these calculation. The two following articles describe the process in greater detail.
Measurement and Correction of Systematic, Odometry Errors in Mobile Robots:
Download Paper 58 (803 KB)
Correction of Systematic Odometry Errors in Mobile Robots:
Download Paper 59 (177 KB)
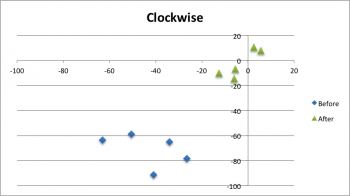
BEFORE CALIBRATION
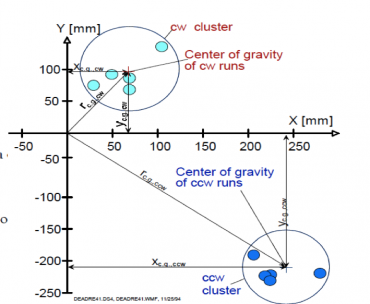
$r_{c.g.,cw}=\sqrt{(X_{c.g.,cw})^2+(Y_{c.g.,cw})^2}$
$r_{c.g.cw} = 83.43 cm $
$r_{c.g.ccw} = 128.67 cm$
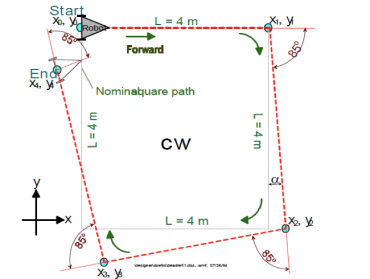
$L = 2 m $
| CLOCKWISE, cw | |||
|---|---|---|---|
| ϵx [cm] | ϵy [cm] | ||
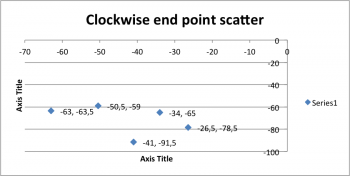
| 1 | -63 | -63.5 | |
| 2 | -50.5 | -59 | |
| 3 | -34 | -65 | |
| 4 | -26.5 | -78.5 | |
| 5 | -41 | -91.5 | |
| Xc.g.= | -43 | Yc.g.= | -71.5 |
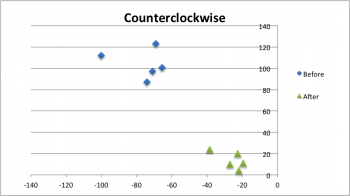
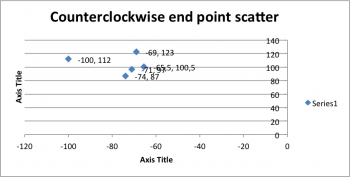
| COUNTERCLOCKWISE, ccw | |||
|---|---|---|---|
| ϵx [cm] | ϵy [cm] | ||
| 1 | -71 | 97 | |
| 2 | -100 | 112 | |
| 3 | -74 | 87 | |
| 4 | -69 | 123 | |
| 5 | -65.5 | 100.5 | |
| Xc.g.= | -75.9 | Yc.g.= | 103.9 |
Calculations
$$\alpha = \frac{x_{c.g.,cw}+x_{c.g.,ccw}}{-4L}\cdot \frac{(180^{\circ})}{\pi}$$
| α = | 851.99 cm |
| 8.5199 m |
$$ \beta = \frac{x_{c.g.,cw}-x_{c.g.,ccw}}{-4L}\cdot \frac{(180^{\circ})}{\pi} $$
| β = | -235.7484 cm |
| -2.357 m |
$$R = \frac{L/2}{sin(\beta /2)} $$
| R = | -48.7 m |
$$E_d = \frac{D_R}{D_L} = \frac{R+b/2}{R-b/2} $$
| b = | 1.524 m |
| $E_d$ = | 0.969 |
$$b_{actual} = \frac{90^{\circ}}{90^{\circ}-\alpha}\cdot b_{nominal} $$
| $b_{actual}$ = | 1.6834 | calibrated value of wheelbase |
| 1.524 | before calibration |
$$c_l = \frac{2}{E_d+1} $$
$$c_r = \frac{2}{(1/E_d)+1} $$
| Correction factor | Before Calibration | After Calibration | |
|---|---|---|---|
| $c_l$ = | 1.0156 | 0.00343 | 0.003484 |
| $c_r$ = | 0.9844 | 0.00324 | 0.003193 |
AFTER CALCULATION
$r_{c.g.,cw}=\sqrt{(X_{c.g.,cw})^2+(Y_{c.g.,cw})^2}$
$r_{c.g.cw} = 4.12 cm$
$r_{c.g.ccw} = 29.35 cm$
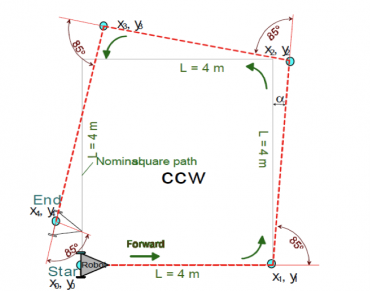
| CLOCKWISE, cw | |||
|---|---|---|---|
| ϵx [cm] | ϵy [cm] | ||
| 1 | -6 | -14.5 | |
| 2 | -12.5 | -10 | |
| 3 | 5.5 | 8 | |
| 4 | -5.5 | -7 | |
| 5 | 2.5 | 10.5 | |
| Xc.g.= | -3.2 | Yc.g.= | -2.6 |
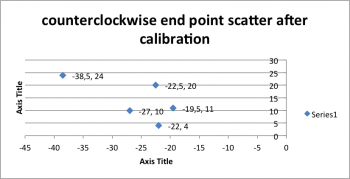
| COUNTERCLOCKWISE, ccw | |||
|---|---|---|---|
| ϵx [cm] | ϵy [cm] | ||
| 1 | -38.5 | 24 | |
| 2 | -27 | 10 | |
| 3 | -19.5 | 11 | |
| 4 | -22.5 | 20 | |
| 5 | -22 | 4 | |
| Xc.g.= | -25.9 | Yc.g.= | 13.8 |